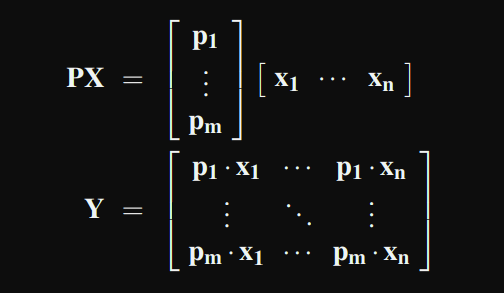Bayesian Stats:
A tutorial introduction to Bayesian Models of Cognitive Dev https://www.sciencedirect.com/science/article/pii/S001002771000291X?casa_token=sCBt5Ty_mG0AAAAA:DdhkeXoWWzUjzQ7SL_02Dk0Qju6JjzylcSqYvmcZZ301SdW9-4ZLGZNb9Nh0F0Xm5_qg1rmh0w
Bayesian Statistics book: https://statswithr.github.io/book/bayesian-inference.html
-
Contrast between Bayesian and Frequentist(source): In real life, here are two ways to elicit a probability that you cousin will get married. A frequentist might go to the U.S. Census records and determine what proportion of people get married (or, better, what proportion of people of your cousin’s ethnicity, education level, religion, and age cohort are married). In contrast, a Bayesian might think “My cousin is brilliant, attractive, and fun. The probability that my cousin gets married is really high – probably around 0.97.”
-
Bayes’ rule is a machine to turn one’s prior beliefs into posterior beliefs
-
As data increases, no matter what the priors, they will converge to reality: The good news is that with the few simple conditions no matter what part distribution you choose. If enough data are observed, you will converge to an accurate posterior distribution. So, two bayesians, say the reference Thomas Bayes and the agnostic Ajay Good can start with different priors but, observe the same data. As the amount of data increases, they will converge to the same posterior distribution
MCMC
https://github.com/davidkipping/sagan2016/blob/master/MCMC.pdf Talk: https://www.youtube.com/watch?v=vTUwEu53uzs
When to use MCMC and regular Bayesian conjugate
If prior and Likelihood are NOT conjugate, that means likelihood x prior = Posterior will not give the family of distributions which is same as Prior.
This summary captures the essence of how to proceed in both scenarios, focusing on whether or not you know the prior distribution and whether or not it is conjugate to the likelihood function.
SBI
SBI lib usage: https://astroautomata.com/blog/simulation-based-inference/
https://www.pnas.org/doi/10.1073/pnas.1912789117 - Frontier of SBI review paper
Pandas to torch_data_loader pitfall
X_train = X_train.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
it is important to drop reset index after u split using train_test_split because the indices are old indices
Intuitive way to think about GLM
So, the simplest model fitting we know is Linear regression. U try to find a line, such that the vertical distances of the points on the line are minimum.
So, another way to see it would be: You are trying to find out mean values. Mean values from which the original data points could have been drawn. Note that the we are assuming a normal distribution here. And the mean value at point x is given by beta_0 + beta_1 x So essentially, we are trying to maximize
exp(- (orginal_Y_1 - beta_0 + beta_1 X_1 )^2) / 2 * sigma^2 times exp(- (orginal_Y_2 - beta_0 + beta_1 X_2 )^2)/ 2 * sigma^2 and so on.
Or we are trying to minimize -log of the above term. (Observe that neg log of the above is same as Sum of Squares error)
So, when does the above method fail?
- When your distribution need not be normal. For example in Bernoulli trials, the outcome is 1 or 0. It is picked from a Bernoulli Distribution NOT a Normal distribution
- beta_0 + beta_1 X. There is no way to restrict this term when we want it. If we want to predict the number of people in a situation, then we want the prediction to be positive. So what if this (beta_0 + beta_1 X) is negative. And another situation is when u want to output a probability btn 0 and 1. How do u restrict (beta_0 + beta_1 X) btn 0 and 1 for a larger value of X.
So, for a model where u don’t restrict the distr to Normal and the model where mean is not just beta_0 + beta_1 X, but a function of beta_0 + beta_1 X is called Generalized Linear Model. If u make the distr as Bernoulli, and the func as Sigmoid. You have logistic regression, which is essentially a Generalized Linear model.
Bernoulli and Binomial
If an experimental as outcome - 1 or 0. Then the distribution of it is called bernoulli, where p is probability of having 1 and 1 - p is probability of having zero.
Binomial - If you repeat the above experiment n times, then probability of having ‘k’ trials with outcome 1 and n - k trials with outcome. Such a prob distrn is called Binomial distr
PMF given by N choose k * p ^k * (1-p)
Why link function in GLM
So that one can regress. For example, X1, X2 are depdendent variables and you want to predict binary outcome. So now, you want X1,X2 as input and probability as output.
u want always the outcome to be between 0 and 1. There is no way u can restrict the outcome between 0 and 1 while u are regressing. So instead u convert to a real value using logit function like log(p / 1-p). And you predict the logit. And later u transform back to probability using e^logit/ 1 + e^logit (Just using inverse func)
IID - Independent and Identically distributed
Why Generalized Linear model instead of simple linear model
Wiki: However, these assumptions are inappropriate for some types of response variables. For example, in cases where the response variable is expected to be always positive and varying over a wide range, constant input changes lead to geometrically (i.e. exponentially) varying, rather than constantly varying, output changes. As an example, suppose a linear prediction model learns from some data (perhaps primarily drawn from large beaches) that a 10 degree temperature decrease would lead to 1,000 fewer people visiting the beach. This model is unlikely to generalize well over different sized beaches. More specifically, the problem is that if you use the model to predict the new attendance with a temperature drop of 10 for a beach that regularly receives 50 beachgoers, you would predict an impossible attendance value of −950. Logically, a more realistic model would instead predict a constant rate of increased beach attendance (e.g. an increase of 10 degrees leads to a doubling in beach attendance, and a drop of 10 degrees leads to a halving in attendance). Such a model is termed an exponential-response model (or log-linear model, since the logarithm of the response is predicted to vary linearly).
Steps for a GLM
(GPT answer)
Certainly! Implementing a Generalized Linear Model (GLM) from scratch involves several key steps:
1. Choose the Distribution for the Response Variable
The first step in creating a GLM is to choose an appropriate probability distribution for the response variable. This choice depends on the nature of the response variable you’re modeling (e.g., Gaussian for continuous data, Poisson for count data, Binomial for binary data, etc.).
2. Select a Link Function
The link function transforms the expected value of the response variable to the linear predictor (a linear combination of the parameters and covariates). Common link functions include:
- Logit for binary data
- Identity for Gaussian distributions
- Log for Poisson distributions
3. Initialize Model Parameters
You will need initial guesses for the parameters of the model. These can be zeros, small random values, or results from a simpler model.
4. Specify the Likelihood Function
The likelihood function describes the probability of observing the given data as a function of the parameters of the model.
5. Develop the Iterative Fitting Algorithm
Most GLMs are fit using an iterative algorithm such as Iteratively Reweighted Least Squares (IRLS) or some optimization technique (like Newton-Raphson, gradient descent, etc.) to find the parameter values that maximize the likelihood function.
For IRLS, which is commonly used in fitting GLMs:
- Calculate the working response variable.
- Calculate the weights.
- Perform a weighted least squares regression to update the parameters.
6. Iterate Until Convergence
The iterative fitting process should continue until the parameters converge within a specified tolerance level. Convergence means that the change in parameter estimates is smaller than the specified threshold.
7. Model Diagnostics and Checking
Once you have fit the model, you need to check the diagnostics to ensure that the model fits the data well. This could include analyzing residuals, checking for overdispersion, and validating assumptions of the GLM.
8. Interpret the Results
After the model is diagnosed and validated, interpret the fitted parameters in the context of the data. This includes estimating the effects, confidence intervals, and potentially predicting new values.
9. Perform Model Validation (Optional)
It may be helpful to validate the model using techniques such as cross-validation or using a hold-out test set to assess the model’s predictive performance.
This is a high-level overview, and each step involves further complexities and considerations, especially when it comes to the specifics of the distribution and link function chosen, as well as the fitting algorithm. Implementing a GLM from scratch is an excellent way to understand these models deeply.
What a linear model assumes and GLM doesn’t
source: 5 min - https://youtu.be/X-ix97pw0xY
Y / X is picked from normal distribution of mean beta_T X. But GLM relaxes that normal condition. They could be from a poisson or other distributions (You do this only in Linear regresssion + Least Square. The Square loss is same as maximizing MLE of normal distriution = max log e ^ - (x - mean)^2 = max -(x - mean)^2 = max - (x - beta_T X)^2 = min (x - beta_T X)
What GLM does is:
- Y/X is now NOT necessarily normal, but from an exponential family of distributions {they are exponential familty bcoz exp shows in prob distr }
- The mean(X) is NOT now just beta_T X, but can be a function of beta_T X
mu = func(beta_T X)
func^ -1(mu) = beta_T X
The link function makes (beta_T X) compatible with some other distribution(say Beronoulli) by transforming it to scale 0 to 1

For example, here the points represent 0/1 - Bernoulli outcome. But if u fit a line, it will asume that future values will always be 1 or greater than 1.
In GLM, mu is NOT necessarily beta_T X so, u try to make it linear by taking some function on mu, like log example mu = a exp(bx) apply log log u = log a + b x. loga = bias, b = coeff1
PCA
X is a matrix where each sample is a vector
P is a matrix whose rows are basis for each sample(column of X)